Managing A Partial Evalution

Introduction

It is critical that the mathematical integrity of an assessment model is maintained and this can be difficult when one or more assessors have the skills, time or inclination to complete only a partial assessment. This article describes various methods that can be used to ensure the integrity of the model is maintained when assessors carry out incomplete assessments.

The Problem Statement

Let’s look at an example. The BUSDOX Technical Assessment Model caters for 1,000 individual selection criteria broken down into 10 Groups with each Group containing 10 Sub-groups and each Sub-group containing 10 Items. Of course, in most situations less than the full complement of 10 Groups will be used as will be the case for Sub-groups and Items. The following figure makes this clear.

Figure 1 – Items within Sub-groups within Groups

To continue with the example shown, we see there are 3 Groups of which 1 Group contains 2 Sub-groups and 2 Groups contain 3 Sub-groups each. The number of Items in each Sub-group is represented in the figure by the horizontal, blue arrows. We call these active criteria. The remaining Groups, Sub-groups and Items are simply labelled “Not Required”.

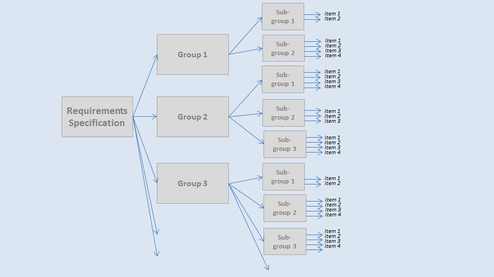
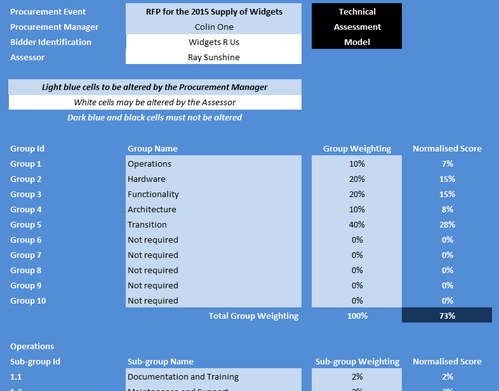
The model allows for a dual weighting to be applied, where the first weighting is of the Groups / Sub-groups and the second is of the Items. Each assessor completes an assessment by rating the performance of a given bidder against all of the active criteria. The model calculates a percentage value which is the score for that bidder by that assessor. This can be seen in the figure below where the normalised score for Widgets R Us by Ray Sunshine is 73%.

e.g.

Before attempting to understand the more complicated case defined in the problem statement, let’s look at the case where all assessors complete a full assessment.

In this straight forward case, it’s a matter of simply averaging the normalised scores.

Figure 2 – Normalised Score for One Bidder by One Assessor

All Full Assessments

Figure 3 – Average Normalised Scores for All Bidder by All Assessors

Let’s assume there are 5 assessors whose normalised scores need to be combined such that the mathematical integrity of the model is maintained. The problem statement is “How do we arrive at a combined score when one or more of the assessors complete only a partial assessment.

One-or-more Partial Assessments

Figure 4 – Complete Assessment on the Left and Partial Group Assessment on the Right

In my view there are only two legitimate cases to consider: one is where one or more Groups are not completed by the assessor; and, the other is where one or more Sub-groups are not completed within a particular Group. We will look at both of these cases below.

As an experienced Procurement Manager I would be very reluctant to allow an assessor to leave me with an incomplete Sub-group assessment. As a Sub-group is highly likely to cover criteria within a single skill set, there is little excuse for not assessing all Items within a Sub-group. If the problem can’t be resolved favourably, the section below entitled Other Alternatives may be of some use.

Partial Group Assessment

Using the example shown in Figure 2, let’s assume, for simplicity of explanation, the first four assessors complete full assessments and the fifth assessor completes an assessment of only Groups 1 to 3. The following figure shows the results of Assessor 1 on the left and those of Assessor 5 on the right.

---

By Assessor 5 not completing the Assessment Model for Groups 4 and 5, the normalised score is taken care of by the model itself by simply not adding in any values for Groups 4 and 5. The more interesting question is how we take care of the averaging process.

It works like this. If all five assessors had completed 100% of the assessment each, we would divide the sum of their normalised scores by five.  If only four assessors had completed 100% of the assessment each, we would divide the sum of their normalised scores by four. In this case we have four assessors completed 100% of the assessment each and one assessor completed only 50% of their assessment (10% + 20% + 20% from the Group Weighting column), we should then divide the sum of the normalised scores by 4.5. If the fifth assessor had completed only the first two Groups (10% + 20% = 30%) we would divide by 4.3.

The general form of the solution is as follows:

e.g.

As mentioned earlier, as a Procurement Manager I would not allow splitting of Sub-groups. If however it was necessary for some reason then the following may be ways to handle it.

Use Another Assessor

Let’s say for example an assessor was determined to make an assessment on Items 3 to 6 in Sub-group 1 of Group 2 but wished to make no other contribution. It may be possible to find another assessor who would be willing to forego their assessment of Items 3 to 6 in Sub-group 1 of Group 2, thus maintaining a full integer in the general form of the solution. 

Share an Assessment

If a number of assessors wish to carry out partial assessments, set aside one Assessment Model for partials only and make sure that you know how much of the 100% has been assessed.

General Form

Use the general form of the solution about. It will work for any combinations however there is an effort required by the Procurement Manager to determine the percentage in the denominator for each partial assessment.

Other Alternatives

Figure 5 – Complete Assessment on the Left and Partial Sub-group Assessment on the Right

In this case we have four assessors completed 100% of the assessment each and one assessor completed only 12% of their assessment (2% + 2% (from Group 1) + 4% + 4% (from Group 2) = 12%), we should then divide the sum of the normalised scores by 4.12.

Partial Sub-group Assessment

The situation where one or more assessors completes a partial Sub-group is virtually the same as above with the slight complication that the Procurement Manager needs to quickly calculate what percentage of the full 100% has been calculated by looking at the Overview Worksheet.

Using the example shown in Figure 5, let’s assume, the first four assessors complete full assessments and the fifth assessor completes an assessment of only Groups 1 to 2 and within Group 1 completes only Sub-groups 1 and 2 and within Group 2 completes only Sub-group2 2 and 3. The following figure shows a complete assessment on the left and the incomplete assessment on the right.

Conclusion

It is perfectly acceptable for assessors to make incomplete assessments in a managed way while maintaining the integrity of the models. There are two points to note:

1/ Assessing less than the full amount of Groups and Sub-groups is fine but Sub-groups should not need to be split.

2/ The general form of the solution always works and is as follows:

admin@busdox.com
www.busdox.com